آنچه که از پیشینیان خوشفکر بشر برای متوازن کردن بناها و صحنه ها و شکوهمند کردن آنها به یادگار مانده است، کشف ترکیب تناسب طلایی است که هر روز ابعاد آن بیش از گذشته کشف می شود. شاید بانیان اصلی آن گمان نمی کردند این کشف به جایی برسد که بتواند رشته های گوناگون اعم از ریاضیات، فیزیک، هنر، اندام شناسی، دکورسازی، صحنه آرایی وغیره را در برگیرد و بتواند برای هر موضوعی حرفی برای گفتن و طرحی برای زیبایی داشته باشد اما چنین واقعیتی به وقوع پیوست و اکنون ترکیب تناسب طلایی به تمامه در خدمت علوم مختلف قرار گرفته است.
علمای دین از آن برای نشان دادن نظم در کائنات، تعمیق شناخت خالق هستی و اثبات عالمانه وجود باریتعالی، دانشمندان زیبایی شناسی برای خلق آثار بدیع، مهندسان برای ساخت بناهای مستحکم و مجلل و متخصصان علوم پزشکی برایی سلامت بخشی به محیط بهره های فراوانی برده اند. از این ترکیب متخصصان امور دفاعی کشورها نیز استفاده کردند تا در دفع خطر به مردم خود خدمت کنند اگرچه مهاجمان نیز از آن برای گشترش حملات خود سوء استفاده کردند.
دانشمندان کشور ما هم که عزم خود را برای رسیدن به توسعه پایدار جزم کرده اند باید دست به دست هم دهند تا با شکافتن مرزهای دانش، جایگاه علمی ایران را که روزگاری در زمینه علمی از ممالک سرآمد بود ،ارتقا بخشند.
تاریخچه:
پیشینه توجه به عدد طلایی نه به زمان فیبوناتچی بلکه به زمانهای بسیار دورتر میرسد. اقلیدس در جلد ششم از سیزده جلد کتاب مشهور خود که در آنها هندسه اقلیدسی را بنا نهاد، این نسبت را مطرح کردهاست .لوکا پاچیولی در سال1509 میلادی کتابی با عنوان نسبت الهی (The Divine Proportion) تالیف کرد. وی در آن نقاشیهایی از لئوناردو داوینچی آورده است که پنج جسم افلاطونی را نمایش میدهند و در آنها نیز به این نسبت اشاره شده است. مصریان، سالها قبل از میلاد از این نسبت آگاه بوده اند و آن را در ساخت اهرام مصر رعایت کردهاند. اما فیبوناچی مسئله ی جالب زاد و ولد خرگوش را مطرح کرد.
دنباله فیبوناچی:
لئوناردو فیبوناچی ایتالیایی تبار اهل پیزا حدود سال 1200 میلادی مسالهای طرح کرد : فرض کنید که یک جفت خرگوش نر و ماده در پایان هر ماه یک جفت خرگوش نر و ماده جدید به دنیا بیاورند ... اگر هیچ خرگوشی از بین نرود ، در پایان یک سال چند جفت خرگوش وجود خواهد داشت ؟ البته در این مسئله میبایست قواعد و اصول فرضی و قراردادی زیر مراعات شوند!
"شما یک جفت خرگوش نر و ماده دارید که همین الآن متولد شده اند؛
خرگوشها پس از یک ماه بالغ میشوند .
دوران بارداری خرگوشها یک ماه است .
هنگامی که خرگوش ماده به سن بلوغ میرسد حتما باردار میشود.
در هر بار بارداری خرگوش ماده یک خرگوش نر و یک ماده میزاید .
خرگوشها تا پایان سال نمیمیرند . "
او برای حل این مسئله به یک سری از اعداد یا بهتر است بگوییم به یک دنباله رسید که.این دنباله عبارت بود از, ... 89،144،233،55،43،12،31،8،5،3،2،1،1،0 که در این دنباله هر عددی (به غیر از صفر و یک اول) حاصل جمع دو عدد قبلی خودش میباشد ، به طور مثال 3+5=8 یا 1+2=3 و .....به این دنباله،دنباله ی فیبوناچی گفته می شود.
نسبت طلایی:
اولین مطلبی که در زمینه ارتباط با دنباله فیبوناچی قابل ذکر است به این قرار است: دنباله را بار دیگر در نظر می بینیم:، 55،43،12،31،8،5،3،2،1،1 نسبت جمله دوم به اول برابر است با 1 نسبت جمله سوم به دوم برابر است با 2 نسبت جمله چهارم به سوم برابر است با 1.5 نسبت جمله پنجم به چهارم برابر است با 1.66 نسبت جمله ششم به پنجم برابر است با 1.6 نسبت جمله هفتم به ششم برابر است با 1.625 نسبت جمله هشتم به هفتم برابر است با 1,615 نسبت جمله نهم به هشتم برابر است با 1,619 نسبت جمله دهم به نهم برابر است با 1,617 ؛ به نظر می رسد که این رشته به عدد طلایی نزدیک می شود. اگر نسبت عدد چهلم این رشته را به عدد قبلی حساب کنیم به عدد 1,618033988749895 می رسیم که با تقریب14 رقم اعشار نسبت طلایی را نشان می دهد .نسبت جملات متوالی به عدد طلایی میل می کند.
نسبت طلایی در ریاضیات و هنر هنگامی است که «نسبت بخش کوچکتر به بخش بزرگتر، برابر با نسبت بخش بزرگتر به کل» باشد.
تعریف دیگر نسبت طلایی این است که «عددی مثبت است که اگر به آن یک واحد اضافه کنیم به مربع آن خواهیم رسید». تعریف هندسی آن چنین است: طول مستطیلی به مساحت واحد که عرض آن یک واحد کمتر از طولش باشد.
تعبیر هندسی دیگر اینگونه است: پاره خطی را در نظر بگیرید و آن را به گونه ای تقسیم کنید که که نسبت بزرگ به کوچک معادل نسبت کل پاره خط به قسمت بزرگ باشد. اگر این معادله ساده یعنی a*b+b=2a2 را حل کنیم (کافی است بجای b عدد یک قرار دهیم بعد a را بدست آوریم) به نسبتی معادل تقریبا” 1.61803399 یا 1.618 خواهیم رسید.

رسم مستطیل طلایی:
جهت رسم یک مستطیل طلایی به نسبت عدد طلایی ابتدا یک مربع به ضلع یک واحد کشیده سپس طبق شکل پائین وسط ضلع پایینی این مربع را پیدا میکنیم . سپس یک قوس با شعاعی به اندازه وسط ضلع پایینی مربع تا گوشه سمت راست بالا میکشیم تا طول مستطیل معلوم شود.
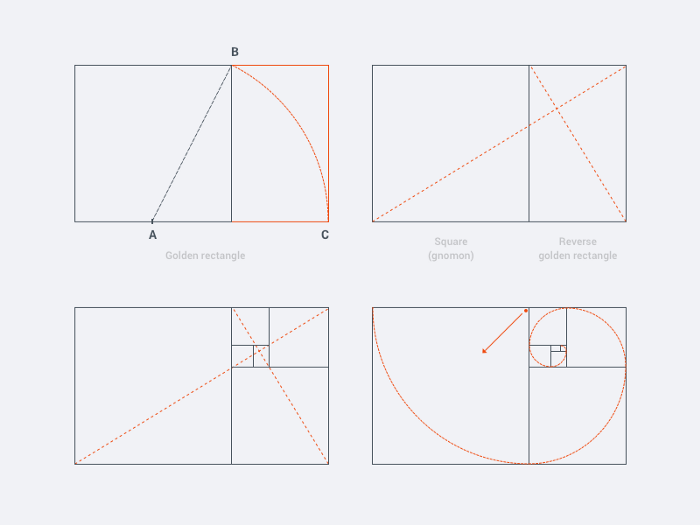
نسبت طلایی در علم زیباشناسی
در سده اخیر ، نسبت های طلایی در علوم پزشکی اهمیت زیادی پیدا کرده اند که بیش از همه مورد استقبال دندان پزشکان و ارتودنتیست ها قرار گرفت. در زیر به برخی از این نسبت های شگفت انگیز چهره انسان می پردازیم.
1: در صورت انسان ، وقتی که دندان ها به هم فشرده نشده باشند و فک پایین در حالت استراحت باشد، خط لب پایین (که با دندان های بالایی مماس است) ، فاصله پایین بینی تا پایین چانه را به نسبت طلایی تقسیم می کند.
2: دیگر نسبت طلایی شناخته شده در دندان ها ، بین چهار دندان جلویی از هر دو سمت است (ردیف فوقانی) البته این نسبت زمانی درست خواهد بود که ردیف دندان ها از روبرو مشاهده شود.
3: دیگر نسبت طلایی کشف شده بین دو دندان پیشین است . مجموع عرض این دو دندان با طول این دندان ها رابطه طلایی دارد.
4: فاصله بین دو چشم انسان با طول هر یک از چشم ها رابطه طلایی دارد.
نسبت طلایی در پزشکی و سلامت
1: مطالعات بر روی نوار قلب افراد سالم نشان داده که بین ارتفاع خطوط و نیز فاصله عرضی پالس ها نسبت طلایی وجود دارد.
2: ایده آل ترین تناسب در صورت ، نسبت طلایی موجود بین طول و عرض مستطیلی است که به صورت محیط می شود. هرگونه انحراف در این تناسب ، نشانه عدم سلامتی کامل است.
A: افرادی که صورتی کشیده تر دارند ، عموما دارای مشکل تنفسی هستند؛ مطالعات انجام شده بیانگر این مطلب است که افرادی که صورتی کشده دارند دارای حفره های سینوسی باریکی هستند بنابراین مجبورند در هنگام فعالیت از راه دهان تنفس کنند. البته امروز این مشکل بوسیله دستگاه های ارتودنسی برطرف شده است.
B: افرادی که صورتی گرد دارند ، مشکلات فکی دارند؛ رشد نامتناسب فک در این افراد موجب اعمال فشار اضافی به مفاصل فک این افراد می شود. بیشتر افراد این گروه از سردرد رنج می برند زیرا قرارگیری نامناسب فک ، موجب می شود که از رسیدن خون به مغز تا حدودی جلوگیری کند. این مشکل نیز بوسیله ارتودنسی قابل درمان است.
در بدن انسان مثالهای بسیار فراوانی از این نسبت طلایی وجود دارد. در شکل زیر نسبت M/m یک نسبت طلایی است که در جای جای بدن انسان می توان آنرا دید. به عنوان مثال نقاطی از بدن که دارای نسبت طلایی هستند:
1: نسبت قد انسان به فاصله ناف تا پاشنه پا
2: نسبت فاصله نوک انگشتان تا آرنج به فاصله مچ تا آرنج
3: نسبت فاصله شانه تا بالای سر به اندازه سر
4: نسبت فاصله ناف تا بالای سر به فاصله شانه تا بالای سر
5: نسبت فاصله ناف تا زانو به فاصله زانو تا پاشنه پا
6: نسبت طلایی گوش انسان
اینها تنها چند مثال از وجود نسبت طلایی در بدن انسان بود که بدن انسان را در حد کمال زیبایی خود نشان می دهد.
نسبت طلایی در طبیعت
1: یکی از تماشایی ترین نمونه های سری فیبوناچی در طبیعت ، بخش مرکزی گل آفتابگردان است . دانشمندان مارپیچ های موجود در بخش مرکزی گل آفتابگردان را مطالعه کردند. در این بین دو سری مارپیچ پیدا شد ؛ یکی در جهت ساعتگرد که عموما کوتاه ترند. این مجموعه شامل 21 بازو می باشد. سری دیگری پادساعتگرد و بلند هستند که شامل 34 بازو می باشد. شگفت انگیزی این دو گروه در این است که این دو سری به صورت شگفت انگیزی به هم متصل شده اند. و دیگر شگفتی در نسبت طلایی بین عددهای یاد شده است. این نسبت ها (صرف نظر از عدد آنها) در آناناس ، میوه درخت کاج و.. . مشاهده شده است.
2."فیلوتاکسیس" (phyllotaxis) علمی است که به مطالعه مکان قرارگیری برگ ها بر روی ساقه می پردازد. تناسبات رعایت شده در رویش برگ گیاهان باعث می شود که نورگیری گیاه به حداکثر برسد و از طرفی دیگر ، آب باران از طریق این برگ ها به سمت ساقه متمایل می شود و بوسیله ساقه به کلیه ریشه ها که در جهات مختلف گسترده شده اند به طور متناسب تقسیم می شود.
برخی چیدمان های متداول درختان منطبق بر سری فیبوناچی:
2:1 نارون ، کاهو ، لیمو
3:1 چنار ، فندق ، شاه توت
5:2 سیب ، گیلاس ، بلوط ، راج ، آلو
8:3 رز ، گلابی ، صنوبر(سپیدار) ، بید
13:5 بادام
از طرف دیگر ، اگر از اختلاف ارتفاع برگ ها صرف نظر کنیم به این نتیجه می رسیم که زاویه چرخش دو برگ متوالی ، به طور کلی" 137,5 است. این زاویه بسیار هوشمندانه محاسبه شده به طوری که بهترین زاویه برای حداکثر بودن نورگیری در برگ های یک گیاه است. که این زاویه نیز خود چند نسبت طلایی را تداعی می کند:
نسبت طلایی دیگر در برگ گیاهان ، نسبت فاصله یک برگ با برگی بالاتر از آن که دقیقا بر آن منطبق است ، با تعداد برگهایی که در این میان قرار دارند ، است . برای نمونه اگر فاصله بین دو برگ که از دید بالا بر هم منطبق هستند 160 میلیمتر باشد ، تعداد برگ هایی که در این فاصله قرار دارند برابر خواهد بود با 10.
3: در انگشتان انسان نیز می توان نسبت طلایی را مشاهده کرد. بزرگ ترین استخوان هر یک از انگشتان با استخوان میانی نسبت طلایی دارد. همین رابطه بین استخوان میانی و استخوان کوچک وجود دارد.
نسبت طلایی و دما:
1: اگر دمای جوش آب را بر 1,618 تقسیم بکنیم عدد 8,61 بدست می آید که دمای استریلیزاسیون (از بین بردن میکروب ها) است.
2: اگر عدد بدست آمده در بالا را دوباره بر عدد فی تقسیم کنیم ، عدد 2,38 بدست می آید که متوسط دمای بدن انسان است.
3: اگر دوباره عدد بدست آمده را بر عدد فی تقسیم کنیم ، عدد 8,23 بدست می آید . این دما (دمای اتاق) مطلوب ترین دما برای فضای داخل یا خارج از خانه است.
نسبت طلایی در جهان هستی
1: حلقه های کاسینی یکی از زیباترین تناسبات طلایی در منظومه ماست. که در آن دو نسبت طلایی دیده می شود.
2: ونوس و زمین نیز به گونه ای جالب این نسبت را یادآور می شوند. در 8 سال زمینی که برابر با 13 سال ونوسی است ، 5 بار مقارنه زمین و ونوس رخ می دهند که این سه ، سه عدد متوالی سری فیبوناچی هستند.
3: زمین با عطارد نیز رابطه ای شگفت انگیز دارد. عطارد هر 87,968 روز زمینی یک بار به دور خورشید می گردد؛ و هر 115,88 روز یک بار با زمین به نزدیک ترین فاصله می رسد.بنابراین حاصل تقسیم 11588/365,24 برابر است با تعداد مقارنه در یک سال . که در 7 سال این تعداد به 22 مقارنه می رسد که بسیار به اعداد سری فیبوناچی نزدیک است.
4: از سوی دیگر ، در اکتبر 2001 ، ناسا شروع به جمع آوری داده هایی در مورد تابش های پس زمینه کیهانی ، مانند نور هایی که از ستاره ها و کهکشان های بسیار دور منتشر می شوند کرد. این داده ها نمایی کلی از جهان را در هنگام زایش به دانشمندان داد. نوسانات تراکم در این تابش ها مسائل بسیار بیشتری در مورد طبیعت فضا به دانشمندان دادند.
ناسا در اکتبر 2003 اولین بررسی بر روی داده های بدست آمده را آغاز کرد و در پایان این بررسی ، یکی از نتایج بدست آمده این بود که جهان ما به شکل یک 12 وجهی منتظم است . و جالب تر از آن این که در 12 وجهی منتظم ، رابطه ضلع با قطر برابر عدد فی است.
نسبت طلایی در اسلام
مسلمانان اجازه نداشتند از تصویر مخلوقات و جانداران در مساجد استفاده کنند. به همین دلیل تصمیم گرفتند ریاضیات را از نو دسته بندی کنند تا راهی برای تزیین مکان پرستش خود بیابند. سری فیبوناچی به صورت وسیع در دکوراسیون اسلامی دیده می شود. به طوری که می توان آن را پایه و اساس هندسه اسلامی دانست.
نسبت طلایی در ایران
برج و میدان آزادی:
طول بنا 63 متر و عرض آن 42 متر است.1.5=63/42 که عددی نزدیک به عدد طلایی می باشد.سبک معماری آن ،طاق بزرگی است که تلفیقی از سبک هخامنشی و ساسانی و اسلامی است که منحنی آن با الهام از طاق کسری است و معماری ایران باستان را تداعی می کند.
بیستون از دوره هخامنشی، کرمانشاه:
به طول 5 و عرض 3 کیلومتر . اعداد 5 و 3 هر دو جزء دنباله ی فیو ناتچی هستند و 1.6=5/3 . ابعاد برجسته کاری 16 در 10 پاست. قامت داریوش 5 پا و 8 اینچ (170سانتی متر) بلندی دارد که هر دو اعداد اعداد فیو ناتچی هستند.
پل ورسک در مازندران:
این پل بر روی رودخانه ی ورسک در مجاورت سواد کوه بنا شده است.بلندی این چل 110 متر و طول قوس آن 66 متر می باشد(1.6=110/66)
مقبره ابن سینا در همدان:
آرامگاه در وسط تالاری مربع شکل قرار گرفته و پل مدور (مارپیچ فیو نا تچی) و پایه های دوازده گانه برج را احاطه کرده اند.سطح حیاط با 3 پله سراسری به ایوان متصل شده است. ایوان باد یواری به ارتفاع 3.2 متر و عرض 1.9 متر به سرای آرمگاه متصل است (1.6=3.2/1.9) .در دو طرف سرسرا، دو تالار قرار دارد. یکی در جنوب که تالار سخنرانی و اجتماعات است.و یکی درشمال که کتابخانه وآرامگاه است.طول تالار کتابخانه 9.45 و عرض آن 5.75 متر است. (1.6=9.45/5.75)
تناسب طلایی در اهرام مصر:
اهرام مصر یکی از قدیمی ترین ساخته های بشری است که در آن هندسه و ریاضیات بکار رفته شده است. مجموعه اهرام گیزا در مصر که قدمت آنها به بیش از 2500 سال پیش از میلاد می رسد یکی از شاهکارهای بشری است که در آن نسبت طلایی بکار رفته است. به این شکل نگاه کنید که در آن بزرگترین هرم از مجموعه اهرام گیزا خیلی ساده کشیده شده است. مثلث قائم الزاویه ای که با نسبت های این هرم شکل گرفته شده باشد به مثلث قائم مصری یا Egyptian Triangle معروف هست و جالب اینجاست که بدانید نسبت وتر به ضلع هم کف هرم معادل با نسبت طلایی یعنی دقیقا” 1.61804 می باشد. این نسبت با عدد طلایی تنها در رقم پنجم اعشار اختلاف دارد یعنی چیزی حدود یک صد هزارم. باز توجه شما را به این نکته جلب می کنیم که اگر معادل فیثاغورث را برای این مثلث قائم الزاویه بنویسم به معادله ای مانند phi+b=2i2 خواهیم رسید که حاصل جواب آن همان عدد معروف طلایی خواهد بود . (معمولا” عدد طلایی را با phi نمایش می دهند) طول وتر برای هرم واقعی حدود 356 متر و طول ضلع مربع قاعده حدودا” معادل 440 متر می باشد بنابر این نسبت 356 بر 220 (معادل نیم ضلع مربع) برابر با عدد 1.618 خواهد شد.
نسبت طلایی در خوشنویسی:
استاد میرعماد با پالایش خطوط پیشینیان و زدودن اضافات و ناخالصی ها از پیکره نستعلیق و نزدیک کردن شگرف نسبتهای اجزای حروف و کلمات، به اعلا درجه هنر زیبایی یعنی نسبت طلایی رسید و قدمی اساسی در اعتلای خط نستعلیق برداشت. با بررسی اکثریت قاطع حروف و کلمات میرعماد متوجه میشویم که این نسبت به عنوان یک الگو در تار و پود حروف و واژه ها وجود دارد و زاویه 63/448 درجه که مبنای ترسیم مستطیل طلایی است، در شروع قلم گذاری و ادامه رانش قلم، حضوری تعیین کننده دارد. این مهم قطعاً در سایه شعور و حس زیبایی شناسی وی حاصل آمده، نه آگاهی از فرمول تقسیم طلایی از دیدگاه هندسی و علوم ریاضی. میرعماد این نسبتها را نه تنها در اجزای حروف بلکه در فاصله دو سطر و مجموعه دو سطر چلیپاها و کادرهای کتابت و قطعات رعایت می کرده است.





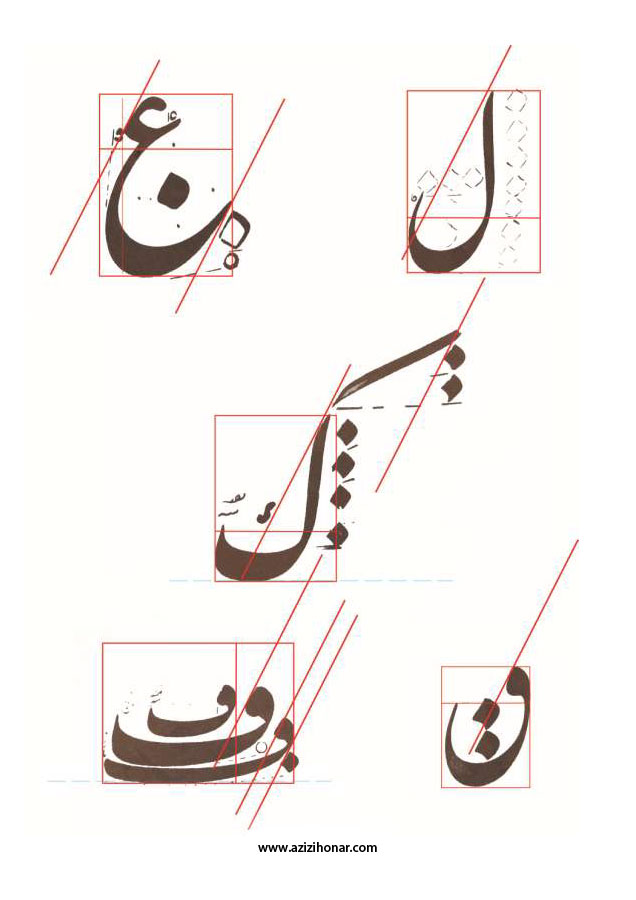







 خوشنویسی یا خطاطی به معنی زیبانویسی یا نوشتن همراه با خلق زیبایی است و فردی که این فرایند توسط او انجام میگیرد خوشنویس (خطاط) نام دارد، بهخصوص زمانی که خوشنویسی حرفهٔ شخص باشد.
خوشنویسی یا خطاطی به معنی زیبانویسی یا نوشتن همراه با خلق زیبایی است و فردی که این فرایند توسط او انجام میگیرد خوشنویس (خطاط) نام دارد، بهخصوص زمانی که خوشنویسی حرفهٔ شخص باشد.